数学において、ボレルの不動点定理(ボレルのふどうてんていり、英: Borel fixed-point theorem)とは、リー=コルチンの定理の一般化である代数幾何学における不動点定理である。Armand Borel (1956) によって証明された。
定理の内容
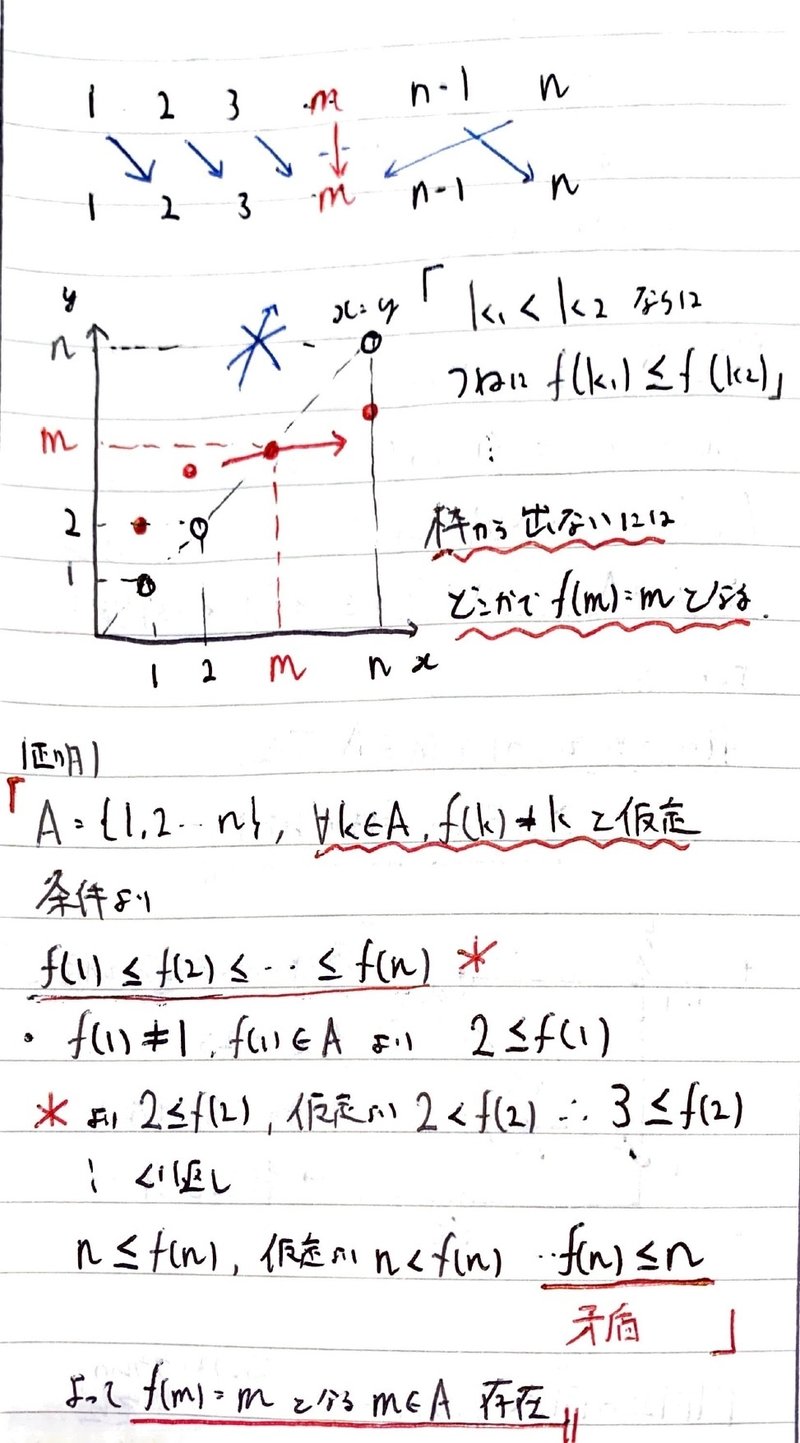
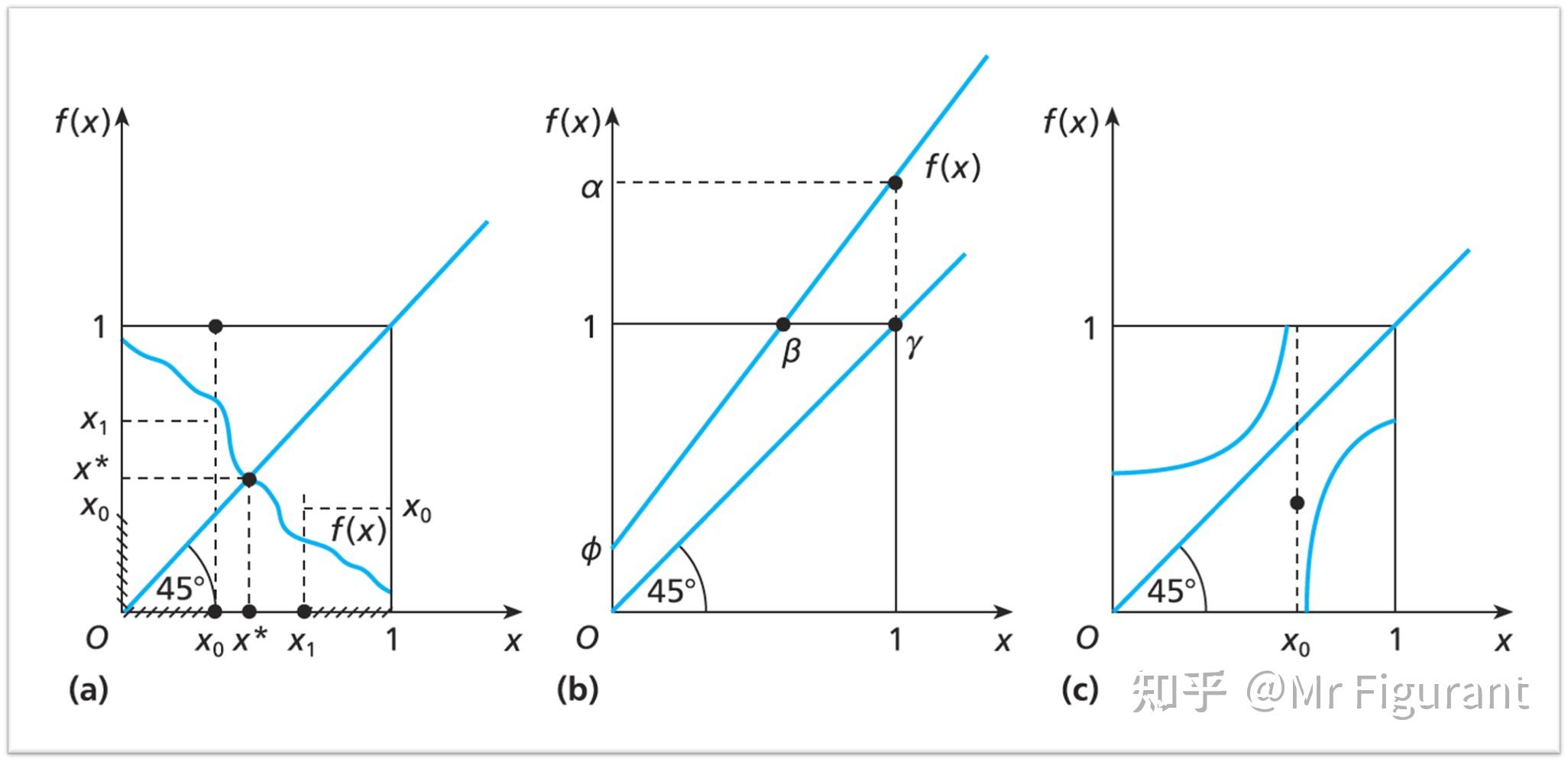
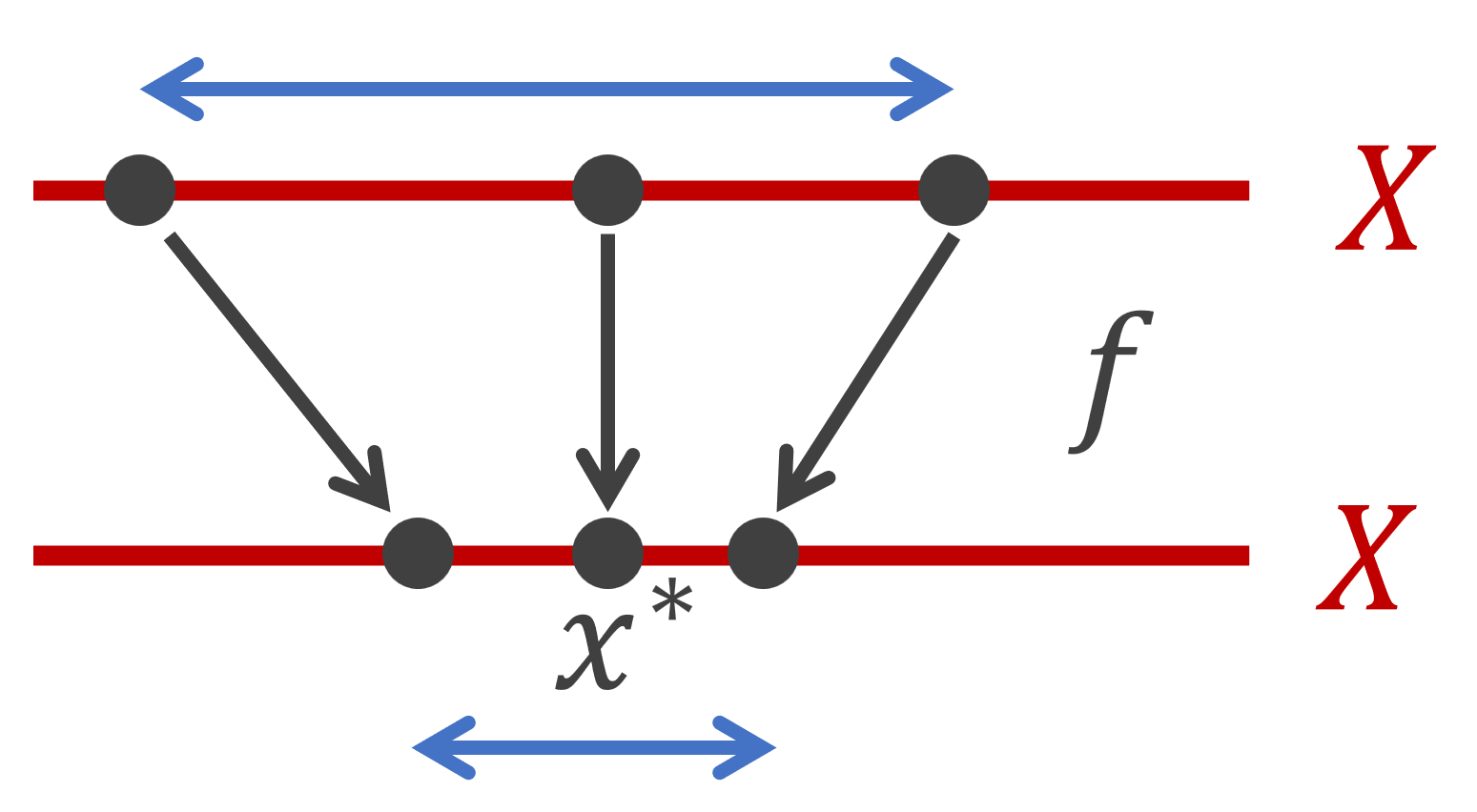
G が代数的閉体 k 上の空でない完備代数多様体 V について正則に作用する連結可解代数群であるなら、V の G 不動点が存在する。
参考文献
- Borel, Armand (1956). “Groupes linéaires algébriques”. Ann. Math. (2) (Annals of Mathematics) 64 (1): 20–82. doi:10.2307/1969949. JSTOR 1969949. MR0093006.
外部リンク
- V.P. Platonov (2001), “Borel fixed-point theorem”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Borel_fixed-point_theorem